ListWeaver - Adjacency Matrix

Status: Completed
vWorker link: C# Algorithm: Adjacency Matrix
Competition start date: 2012.06.27
Competition end date: 2012.07.10
Download associated files (version 1.4)

Please make sure to read the Welcome page for general competition guidelines.
If you would like to participate in this competition please register an account on vWorker.com

Update:

2012.07.09: Corrected Example 2. Added workings

2012.07.09: Added more explanation to the matrix approach, under the "Matrix representation" section.
2012.07.09: Updated files to version 1.4
2012.11.30: Looks like this problem should be easy to solve now with csparse library

This competition is based on the ListWeaver competition. The problem description, unit tests and benchmarks are exactly the same, however the solution has to use an adjacency matrix representation of the problem and find a transformation matrix which will return the correct result.

Some useful links are:

- Wikipeida - Adjacency matrix

- Search for Adjacency matrix and eigenvalues.

3rd party, open source .NET libraries can be used if required. If you do use a 3rd party library please let me know which one it is when submitting your solution.

Extra Example 1:

Input:
Purple
Green
Orange,Purple
Green,Purple

Result:
Green, Orange, Purple

Extra Example 2:

Input:
Blue
Bronze, Yellow, Purple
Black, Orange
Red, Blue, Gold
Silver, Blue
Bronze, Blue

Shown below is the working of the solution by adding one yarn at a time. When the final yarn "Bronze, Blue" is added, the "Bronze" colour gets promoted the first element, since "Bronze" already appears in the second list, therefore takes precedence over colours in subsequent lists.

Result:
Bronze, Red, Silver, Blue, Yellow, Purple, Black, Orange, Gold

Extra Example 3:

Input:
Blue
Bronze, Yellow, Purple
Black, Orange
Red, Blue, Gold
Silver, Blue

Result:
Red, Silver, Blue, Bronze, Yellow, Purple, Black, Orange, Gold

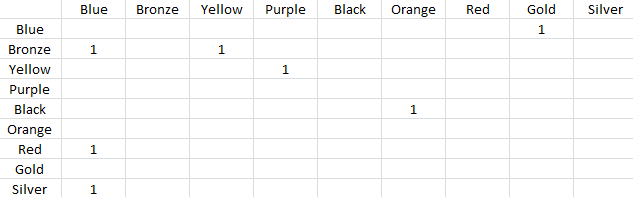
Matrix Representation:

If we look at example 2, and represent it in matrix form, we will get the following:

We obtain this matrix by taking the colours as they appear in each list but we remove duplicates.

The "1" value represents an edge connecting one colour to another. So we can see Bronze is connected to Blue in one list, and that Bronze is connected to Yellow in another list. Yellow in turn is connected to Purple. etc...

In order to get the correct sequence we process each column in order as they appear. We start with Blue.

If there are any "1"s in the column we process the rows in order and add the colour of the column at the end.

Which means that after column "Blue" we get:

Bronze, Red, Silver, Blue

We now move onto the second column "Bronze". There is nothing in this column and Bronze is already contained in the resulting list so we can skip it.

Column "Yellow" has a "1" on the "Bronze" row, but "Bronze" is already contained in the resulting list, so we add "Yellow" to the end of the list:

Bronze, Red, Silver, Blue, Yellow

Column "Purple" is similar. It has a "1" in the yellow row, but yellow is already contained in the resulting list so we just add Purple to the end:

Bronze, Red, Silver, Blue, Yellow, Purple

The "Black" column has no entries so "Black" simply gets added to the end of the list:

Bronze, Red, Silver, Blue, Yellow, Purple, Black

The "Orange" column has a "Black" entry, but black is already in the list, so add Orange to the end of the list:

Bronze, Red, Silver, Blue, Yellow, Purple, Black, Orange

The "Red" column has no entries but it is already contained in the list, so we can skip it.

The "Gold" column has a "Blue" entry, but "Blue" is already contained in the list, so Gold goes to the end of the list:

Bronze, Red, Silver, Blue, Yellow, Purple, Black, Orange, Gold

Finally we get to the "Silver" column, which has not entries and is already contained in the list, so the final results is:

Bronze, Red, Silver, Blue, Yellow, Purple, Black, Orange, Gold 

Reformatting the result in matrix form we get:

The aim of this competition is to find a transformation matrix which will take the first matrix shown above, and return an upper triangular matrix as illustrated here.

This is a typical matrix decomposition problem and must be solved using matrix functions. (such as inverse, transpose etc...)